Polynomial Prediction Problems#

When fitting the \(\textrm{CO}_2\) in previous sections, we have used polynomial models. This section is a slight deviation, where we take three future scenarios, defined by the Special Report on Emission Scenarios(SRES) and give them ‘back of the envelope’ functional forms. With this we explore some problems associated with polynomial fitting and two methods that can be used to tackle this problem.

The model will have three separate cases. As discussed before they are as follows:

  • A1B) Continued growth in emission Rates.

  • A1T) Net-zero by 2030, no further reductions.

  • B1) Net-zero by 2030, and then reducing total atmospheric carbon at the same rate it is currently produced.

\(\textrm{CO}_2\) Concentration Models#

In the section, a polynomial model, eq.(14) with a trigonometric addition was developed to characterize the Mauna Loa \(\textrm{CO}_2\) concentration, which closely follows the global average trend. Using the model without the trigonometric terms will be the basis for this section.

"""
This block defines the functions used to approximate the scenarios, and
an error functon.
"""
def lb_ub(values, sigma, factor=1):
    lb = values - sigma * factor
    ub = values + sigma * factor
    return lb, ub


# Models
def A1T(x, p_0, p_1, p_2, p_3, translation=0):
    emissions_stop = np.where(x + translation >= 2030)[0]
    f_eval = p_0 + p_1 * x + p_2 * x**2 + p_3 * x**3
    f_eval[emissions_stop[0] :] = f_eval[emissions_stop[0] - 1]
    return f_eval


def B1(x, p_0, p_1, p_2, p_3, translation=0):
    emissions_stop = np.where(x + translation >= 2030)[0]
    f_eval = p_0 + p_1 * x + p_2 * x**2 + p_3 * x**3
    f_neg = (
        2 * f_eval[emissions_stop[0] - 1]
        - p_0
        - (p_1 * x + p_2 * x**2 + p_3 * x**3)
    )
    f_eval[emissions_stop[0] - 1 :] = f_neg[emissions_stop[0] - 1 :]
    return f_eval


def A1M(x, p_0, p_1, p_2, p_3):  # A1M
    return p_0 + p_1 * x + p_2 * x**2 + p_3 * x**3

The Problem with Polynomials#

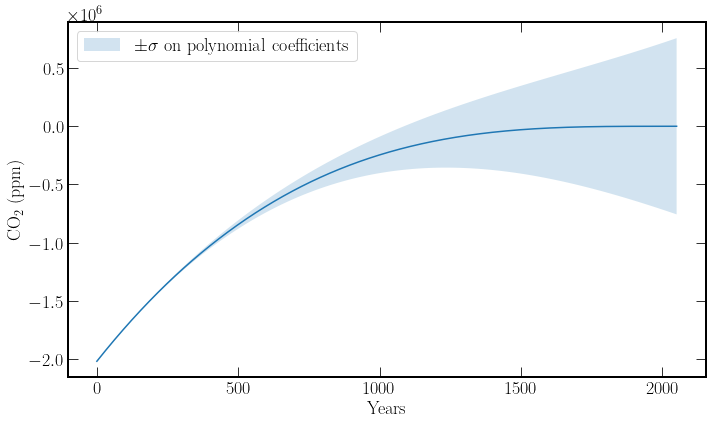
Problems arise when fitting polynomials of order greater than one, minor parameter tweaks to the higher powers’ constants cause large deviations in the value of the function. This can be seen below in the figure. The figure plots the cubic fit from eq.(14) \(\pm 2\sigma\). The time axis is extended to show that it is a polynomial fit and not just a fill. This problem is especially apparent as the data, \(\textrm{CO}_2\) concentration data, is rather linear, and thus there is a moderate uncertainty on the \(x^2, x^3\) terms.

"""
Printing the fractional error on the fit coefficients.
"""
df = pd.DataFrame(abs(poly_fit / poly_error))
df.columns = ["Fit_Value/Error"]
df
Fit_Value/Error
c 2.893789e+15
p_1 3.365573e+15
p_2 1.149817e+01
p_3 1.161567e+01 
time = np.linspace(0, 2050, 1000)
lb_coef, ub_coef = lb_ub(poly_fit, poly_error)
plt.figure(figsize=(10, 6))
plt.plot(time, A1M(time, *poly_fit))
plt.fill_between(
    time,
    A1M(time, *lb_coef),
    A1M(time, *ub_coef),
    alpha=0.2,
    label="$\pm \sigma$ on polynomial coefficients",
)
plt.ylabel(r"$\textrm{CO}_2$ (ppm)")
plt.xlabel("Years")
plt.legend(loc="upper left");
../_images/3models_7_0.png

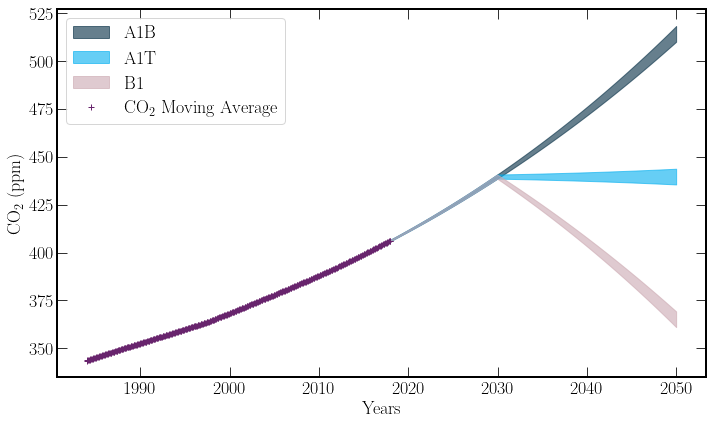
To solve this problem, the \(x\) values of the training data, years, can be translated so that they center about zero. Thus the deviations due to small parameter changes are not as large.

Alternatively, a natural spline fit could be used, treating the extrapolation as linear, and thus the range of values inside the \(2\sigma\) interval would not diverge as rapidly.

# x values
time = np.linspace(1985, 2050, 1000) - 2000
# Loading CO2 moving averages caluclated previously
co2_ave = pd.read_csv(
    "../output_files/co2_10_moving_average.csv", header=0, index_col=0
)
co2_std = pd.read_csv(
    "../output_files/co2_10_moving_std.csv", header=0, index_col=0
)
co2_mov_fit, co2_mov_cov = curve_fit(
    A1M,
    co2_ave["decimal"] - 2000,
    co2_ave["average"],
    sigma=co2_std["average"],
)
# 2 sigma deviation from fit
co2_mov_error = np.diagonal(co2_mov_cov) ** 0.5
co2_lb_mov, co2_ub_mov = lb_ub(co2_mov_fit, co2_mov_error, factor=2)
sigma = A1M(time, *co2_ub_mov) - A1M(time, *co2_mov_fit)
# Plotting
plt.figure(figsize=(10, 6))
# Models
plt.fill_between(
    time,
    A1M(time, *co2_lb_mov),
    A1M(time, *co2_ub_mov),
    color=colours.durham.ink,
    alpha=0.6,
    label="A1B",
)
plt.fill_between(
    time,
    A1T(time, *co2_mov_fit, translation=2000) - sigma,
    A1T(time, *co2_mov_fit, translation=2000) + sigma,
    color=colours.durham.blue,
    alpha=0.6,
    label="A1T",
)
plt.fill_between(
    time,
    B1(time, *co2_mov_fit, translation=2000) - sigma,
    B1(time, *co2_mov_fit, translation=2000) + sigma,
    color=colours.durham.pink,
    alpha=0.6,
    label="B1",
)
# Data
plt.plot(
    co2_ave["decimal"] - 2000,
    co2_ave["average"],
    linestyle="",
    marker="+",
    color=colours.durham.purple,
    label=r"$\textrm{{CO}}_2$ Moving Average",
)
# Formatting
plt.xticks(range(-10, 60, 10), range(1990, 2060, 10))
plt.legend(loc="upper left")
plt.xlabel("Years")
plt.ylabel(r"$\textrm{{CO}}_2$ (ppm)");
../_images/3models_10_0.png

The Natural Cubic Spline#

This section is a mild detour because this technique is not used in the model. Nevertheless, a spline fit can be helpful in scenarios where smoothing is particularly needed, or a trend is difficult to visualize. Albeit, the traditional cubic splines’ extrapolation power is slightly lacking.

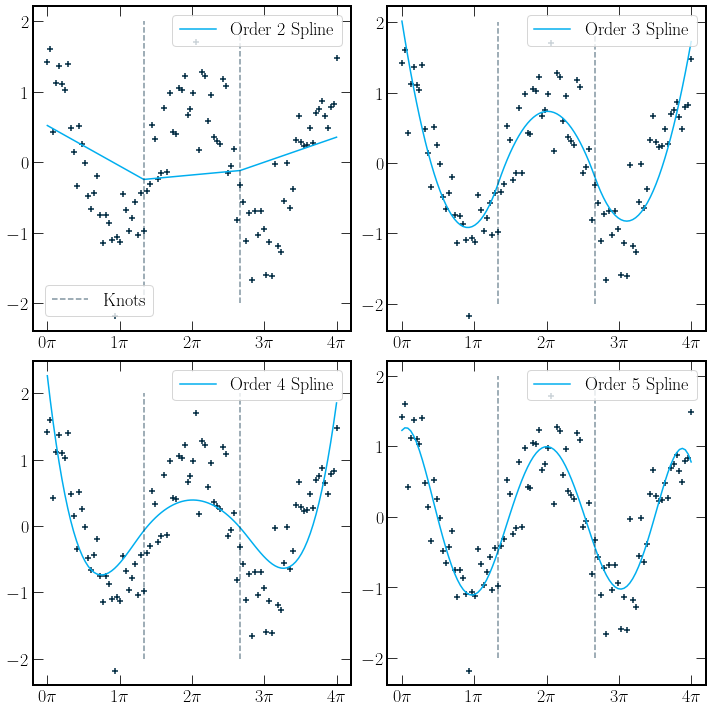
As defined in [HTF09], a spline is piecewise polynomials of order \(m\) with \(m-2\) continuous derivatives. The order-\(m\) spline provides a function, which if defined by the degrees of freedom, has a fixed number of knots, points at which the polynomial changes. In the plot below, spline fits of \(\cos(x)\) with Gaussian noise are plotted. There are two knots for all splines. A dashed grey line indicates the position of the knots. The degrees of freedom for a spline

\[\nu = (knots+1)\cdot m-(knots)\cdot 3 \]

The \(knots+1\) term comes from the number of separate polynomials. There are 3 constraints per knot; where \(x_k\) is the knot postition, the constraints are as follows

\[\begin{split} \begin{aligned} f(x_k^-) & = f(x_k^+), \\ f'(x_k^-) & = f'(x_k^+), \\ f''(x_k^-) & = f''(x_k^+). \end{aligned}\end{split}\]

The implementation of the splines below is using a least-squares fitting method. A natural spline extension can be used if the spline fit is used as a predictive model for data in unseen regions. A natural spline has a first-degree polynomial applied to regions outside the training data range. These lines are continuous and have continuous first derivatives.

Typically order-\(4\) splines are used.

"""
Here we demonstrate using the spline fitting provided by scipy on a small
section of the seasonal data, to demonstrate how flexible they can be.
"""
fig, ax = plt.subplots(2, 2, figsize=(10, 10))
x = np.linspace(0, np.pi * 4, 100)
xs = np.linspace(0, np.pi * 4, 5)
spline_knots = np.linspace(0, np.pi * 4, 4)[1:-1]
y = np.cos(x) + np.random.randn(100) * 0.4
k = 0
for i in range(2):
    for j in range(2):
        k += 1
        spline = LSQUnivariateSpline(
            x,
            y,
            t=spline_knots,
            k=k,
        )
        ax[i, j].scatter(x, y, color=colours.durham.ink)
        ax[i, j].plot(
            x,
            spline(x),
            label=f"Order {k+1} Spline",
            color=colours.durham.blue,
        )
        ax[i, j].set_xticks(xs)
        ax[i, j].set_xticklabels([f"{int(i/np.pi)}$\pi$" for i in xs])
        ax[i, j].legend(loc="upper right")
        for l in spline_knots:
            line = ax[i, j].plot(
                [l, l],
                [-2, 2],
                color=colours.durham.ink,
                alpha=0.5,
                linestyle="--",
                label="Knot",
            )
fig.legend(line, ["Knots"], bbox_to_anchor=(-0.75, 0.59, 0.98, 0.02))
fig.tight_layout()
../_images/3models_12_0.png