Predictive Modeling
Contents
Predictive Modeling#
One of the critical uses of data recorded in the past is to attempt to make inferences about the future. Making predictions about future events on time series data can be done by forming a model on historical data.
An introductory example of the general methodology of data-driven predictions using partitioning data into; training, validation and testing sections is explored. These sections are used as follows; the data is used to derive a model from the training data. Next, this model is tested on available validation data. Finally, the model is applied to the testing data to predict its behaviour.
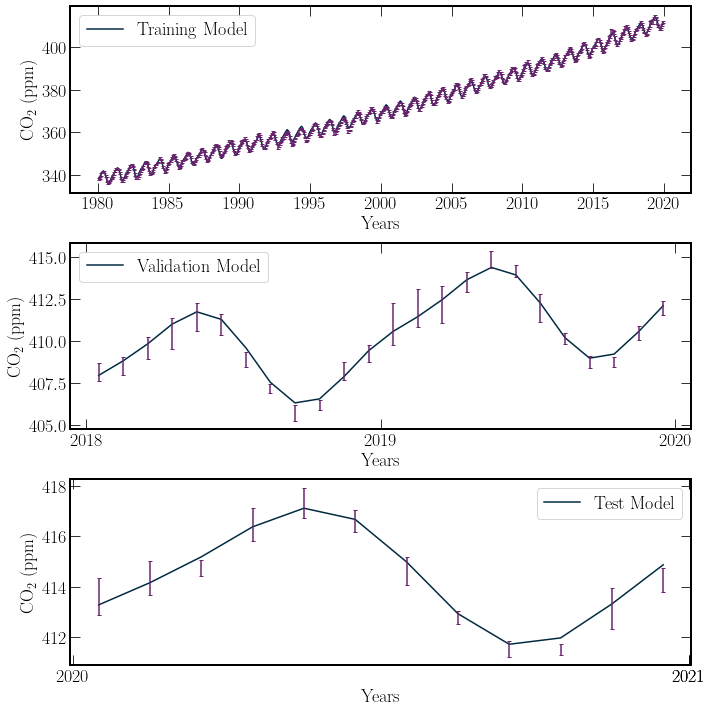
A straightforward example of predictive modelling using linear regression is taken from the previous section and walked through. The question is to test if there is an observable drop-in \(\textrm{CO}_2\) from the pandemic. In the previous section, a model was derived using least-squares regression and Fourier series of the form eq.model. In this example, the free coefficient of the model will be discerned from the period from 1980 up to 2018. This period gives a large window to learn from to avoid learning overly patterns unique to a few years, while also providing a good fit with the validation window of \(2018, 2019\).
When performing any supervised prediction task, a training data set is selected. A training set is data in which the independent and dependent variables are known. In the example of detecting covid, the form of the predicted quantity is slightly obscured, ie the occurrence of an anomalous change in \(\textrm{CO}_2\) concentration. However, when modelling of \(\textrm{CO}_2\) concentration, \(\textrm{CO}_2\) concentration and time are the dependent and independent variables, respectively. The model is then built from this data. For least-squares fitting, this constitutes determining the form of the function and evaluating the free coefficients.
Using the previously developed model, the validation data is then investigated. This must not overlap with the training data. In the global \(\textrm{CO}_2\) data, using the years \(2018, 2019\) provides a period as similar as possible to the test window \(2020, 2021\) asides from the pandemic anomaly being tested for. The quality of the model is then assessed on the validation data. Because the actual value of the validation data is known(There were no pandemics), the model’s efficacy can be assessed here using the \(\chi^2\) metric.
If the model’s behaviour on the validation set is satisfactory. Then the model can be used to investigate the test case. If there was a significant deviation from eq.model in 2020, then the presence of the pandemic can be shown.
def model(x, a_0, a_1, omega_0, omega_1, c, p_1, p_2, p_3):
polynomial = x * p_1 + x**2 * p_2 + x**3 * p_3
trig = a_0 * np.cos((x + 1 / 2) * 2 * np.pi * omega_0) + a_1 * np.cos(
(x + 1 / 2) * 2 * np.pi * omega_1
)
return c + trig + polynomial
# Training Set
test_years = [i for i in range(1980, 2020)]
mask = np.isin(co2_data_ml["year"], test_years)
train_co2_data = co2_data_ml.iloc[mask]
# Validation Set
val_years = [i for i in range(2018, 2020)]
mask = np.isin(co2_data_ml["year"], val_years)
val_co2_data = co2_data_ml.iloc[mask]
# Test Set
test_years = [i for i in range(2020, 2021)]
mask = np.isin(co2_data_ml["year"], test_years)
test_co2_data = co2_data_ml.iloc[mask]
# Fitting
model_fit, model_error = scipy.optimize.curve_fit(
model,
co2_data_ml["decimal date"],
co2_data_ml["average"],
sigma=co2_data_ml["sdev"],
p0=[5, 5, 1, 2, -2 * 10**6, 3 * 10**3, 0, 0,], # Inital Parameter Guess
)
# chisq
model_ml = model(co2_data_ml["decimal date"], *model_fit)
model_residuals = model_ml - co2_data_ml["average"]
chisq_model = np.sum((model_residuals / co2_data_ml["sdev"]) ** 2)
nu_model = co2_data_ml["average"].shape[0] - len(model_fit)
p_model = stats.chi2.sf(chisq_model, nu_model)
chi_crit = stats.chi2.isf(0.05, nu_model)
class FittedModel:
"""
Here we define a Fitted model class, because we are testing multiple
models of the same form, it makes sense to build a tool to speed up the
process of fitting the model and calculating values of interest.
The python class, method framework is a great way of implementing a
task like this.
If this were to be a larger project, one might write the class in a
separate file and then import it as and when you need it.
"""
def __init__(
self, fn, x, y, sigma=None, p0=None, name=None, fit_coefs=None
):
self.fn = fn
self.x = x
self.y = y
self.sigma = sigma
self.p0 = p0
self.name = name
if fit_coefs:
self.fit_coefs, self.fit_errs = fit_coefs
self.fit_errs = None
else:
self.fit_coefs, self.fit_cov = self.get_fit()
self.fit_errs = np.diagonal(self.fit_cov) ** 0.5
def get_fit(self) -> Tuple:
"""Applies scipy.optimize.curve_fit() to the passed args.
Returns:
fit_coefs array, correlation_array
"""
model_fit, model_error = scipy.optimize.curve_fit(
self.fn, self.x, self.y, sigma=self.sigma, p0=self.p0
)
return model_fit, model_error
def fit_data(self):
"""Returns the fitted function evaluated on x"""
return self.fn(self.x, *self.fit_coefs)
def get_chi2(self) -> int:
"""Returns the chi^2 value of the model"""
fit = self.fit_data()
residuals = fit - self.y
if self.sigma is not None:
chi2 = np.sum((residuals / self.sigma) ** 2)
else:
print("No uncertainty, using expectation.")
print("Expectation of the values is: E(residuals)")
chi2 = np.sum((residuals / np.mean(residuals)) ** 2)
return chi2
def get_nu(self) -> int:
"""Returns the degrees of freedom of the model"""
return len(self.x) - len(self.fit_coefs)
def get_sf(self) -> int:
"""Returns P(chi^2 > chi^2_min)"""
chi_min = self.get_chi2()
nu = self.get_nu()
return scipy.stats.chi2.sf(chi_min, nu)
def print_errors(self):
"""Prints the model's coefficients associated errors"""
coef_names = inspect.getfullargspec(self.fn).args
for i, (value, error) in enumerate(
zip(self.fit_coefs, self.fit_errs)
):
if error:
print(f"{coef_names[1+i]} = {value:.2} +_ {error:.1}")
else:
print("No error. The model was fitted on other Data")
"""
Here we use the FittedModel class on our data. As you can see rather
than writing the same code over and over again this interface once built,
saves time and effort.
"""
train = FittedModel(
model,
train_co2_data["decimal date"],
train_co2_data["average"],
sigma=train_co2_data["sdev"],
p0=[5, 5, 1, 2, 0, 0, 0, 0],
name="Training Model",
)
test = FittedModel(
model,
test_co2_data["decimal date"],
test_co2_data["average"],
sigma=test_co2_data["sdev"],
name="Test Model",
fit_coefs=train.get_fit(),
)
val = FittedModel(
model,
val_co2_data["decimal date"],
val_co2_data["average"],
sigma=val_co2_data["sdev"],
name="Validation Model",
fit_coefs=train.get_fit(),
)
print("Training Model Co-efficients")
train.print_errors()
Training Model Co-efficients
a_0 = 2.9 +_ 0.04
a_1 = 0.82 +_ 0.04
omega_0 = 1.0 +_ 1e-06
omega_1 = 2.0 +_ 4e-06
c = -2e+06 +_ 2e+05
p_1 = 3.1e+03 +_ 3e+02
p_2 = -1.5 +_ 0.1
p_3 = 0.00026 +_ 2e-05
Problems with error on \(P_0\) and \(P_1\)#
The error on both quantities is astronomically high, around 10%. Further, it can be shown that it is an inaccurate measurement. If one changes the starting position for these quantities, the p0 kwarg for scipy.optimize.curve_fit, the results do not oscillate around the obtained values indicating that the distribution of possible values is much tighter than the actual result. A better estimate of such errors can be determined by performing the fit with random start values centered around the obtained value.
C coefficient:-2e+06 +_ 7e-10
P_1 coefficient:3e+03 +_ 5e-13
# params
labels = ["a_0", "a_1", "omega_0", "omega_1", "c", "p_1", "p_2", "p_3"]
model_fit_params = pd.Series(train.fit_coefs, index=labels)
fname = "../output_files/co2_model_parameters.csv"
model_fit_params.to_csv(fname)
# errors
model_cov_frame = pd.Series(train.fit_errs, index=labels)
fname = "../output_files/co2_model_parameters_errors.csv"
model_cov_frame.to_csv(fname)
for model_ in [train, val, test]:
print(model_.name)
print(f"chi^2 = {model_.get_chi2():.4}")
print(f"chi^2/nu = {model_.get_chi2()/model_.get_nu():.4}")
print(f"P(chi^2 > chi^2_min) = {model_.get_sf():.4}")
print("")
Training Model
chi^2 = 1.005e+03
chi^2/nu = 2.134
P(chi^2 > chi^2_min) = 7.862e-41
Validation Model
chi^2 = 13.67
chi^2/nu = 0.8541
P(chi^2 > chi^2_min) = 0.6236
Test Model
chi^2 = 9.291
chi^2/nu = 2.323
P(chi^2 > chi^2_min) = 0.05423
Results#
The output \(\chi^2\) statistics for the training model are to be desired, with a very low probability that the model demonstrates a good fit. However, This is not particularly important for the current test. Inspecting the performance of the model on the validation period, the model provides a good fit. This is exemplified by the \(P(\chi^2 \geq \chi^2_{min};\nu) = 0.63\), well inside a significance level of 5 percent. This strong agreement between the validation data and the model suggests that the model is extended into the testing regime.
In the testing regime, the \(P(\chi^2 \geq \chi^2_{min};\nu) = 0.055\). This \(P\) value indicates that approximately 5% of the time, the random variable normalised residuals would be distributed in such a manner. This extrapolation is pushing the bounds of the model. In this case, there is insufficient evidence to say that there has been a noticeable downwards trend in \(\textrm{CO}_2\) production over the year \(2020\).
fig, ax = plt.subplots(3, 1, figsize=(10, 10))
fig.subplots_adjust(hspace=0.4)
dur_cycle = cycler(
color=[colours.durham.ink, colours.durham.purple, colours.durham.red]
)
for i, model_ in enumerate([train, val, test]):
# Formatting
ax[i].set_xlabel("Years")
ax[i].set_ylabel(r"$\textrm{CO}_2$ (ppm)")
ax[i].set_prop_cycle(dur_cycle)
# Data
ax[i].plot(model_.x, model_.fit_data(), label=model_.name)
ax[i].errorbar(model_.x, model_.y, model_.sigma, linestyle="")
ax[i].legend()
ax[1].set_xticks([2018, 2019, 2020])
ax[2].set_xticks([2020, 2021, 2021])
[<matplotlib.axis.XTick at 0x7f3a0a9e5480>,
<matplotlib.axis.XTick at 0x7f3a0a9e5450>,
<matplotlib.axis.XTick at 0x7f3a0a9e5330>]
Discussion#
The linear-regression model developed in the previous section does not account for any global effects that vary the average behaviour of the \(\textrm{CO}_2\) concentration in the previous section. When using the \(\chi^2\) statistic, this returns very poor fits over many years due to significant variances, exemplified by the 90s. However, a small window representing the general overall trend without high variance, like the period of 2018 and 2019, can present a good fit. Towards the end of the year 2021, the residuals of the data points are all negative. This could be the presence of Covid-19; however, the residuals are similar in size to the uncertainty, resulting in the high \(\chi^2\) value.
More can be read about using the \(\textrm{CO}_2\) concentration in the atmosphere to detect the pandemic.
Note
The TLDR of the article from the NOAA, is that global \(\textrm{CO}_2\) concentrations are buffered by release from the ocean and that fires in the southern hemisphere, could have offset the \(\textrm{CO}_2\) emission decrease.

